On Memorization of Large Language Models in Logical Reasoning

How to Measure Memorization in Reasoning Tasks

A proposed memorization metric for reasoning task, and a new logical reasoning dataset.

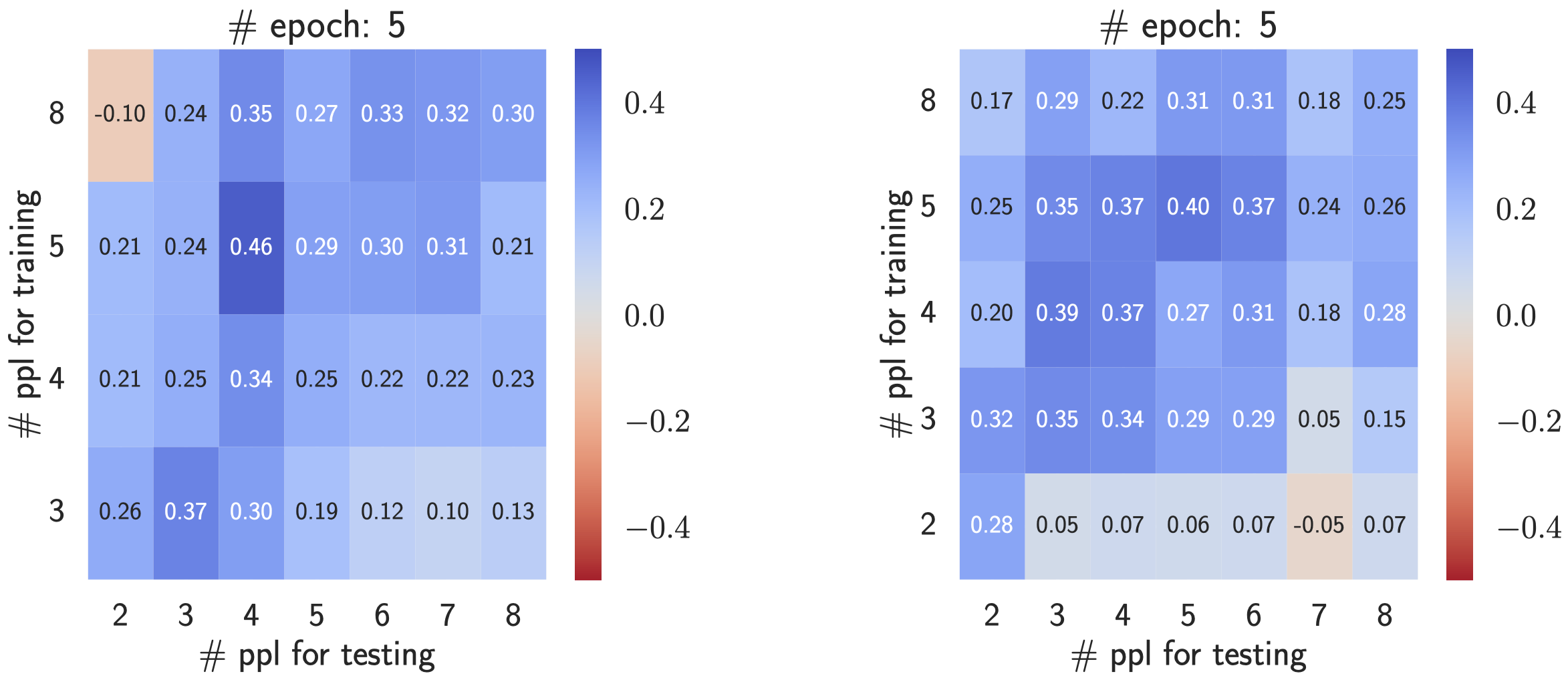
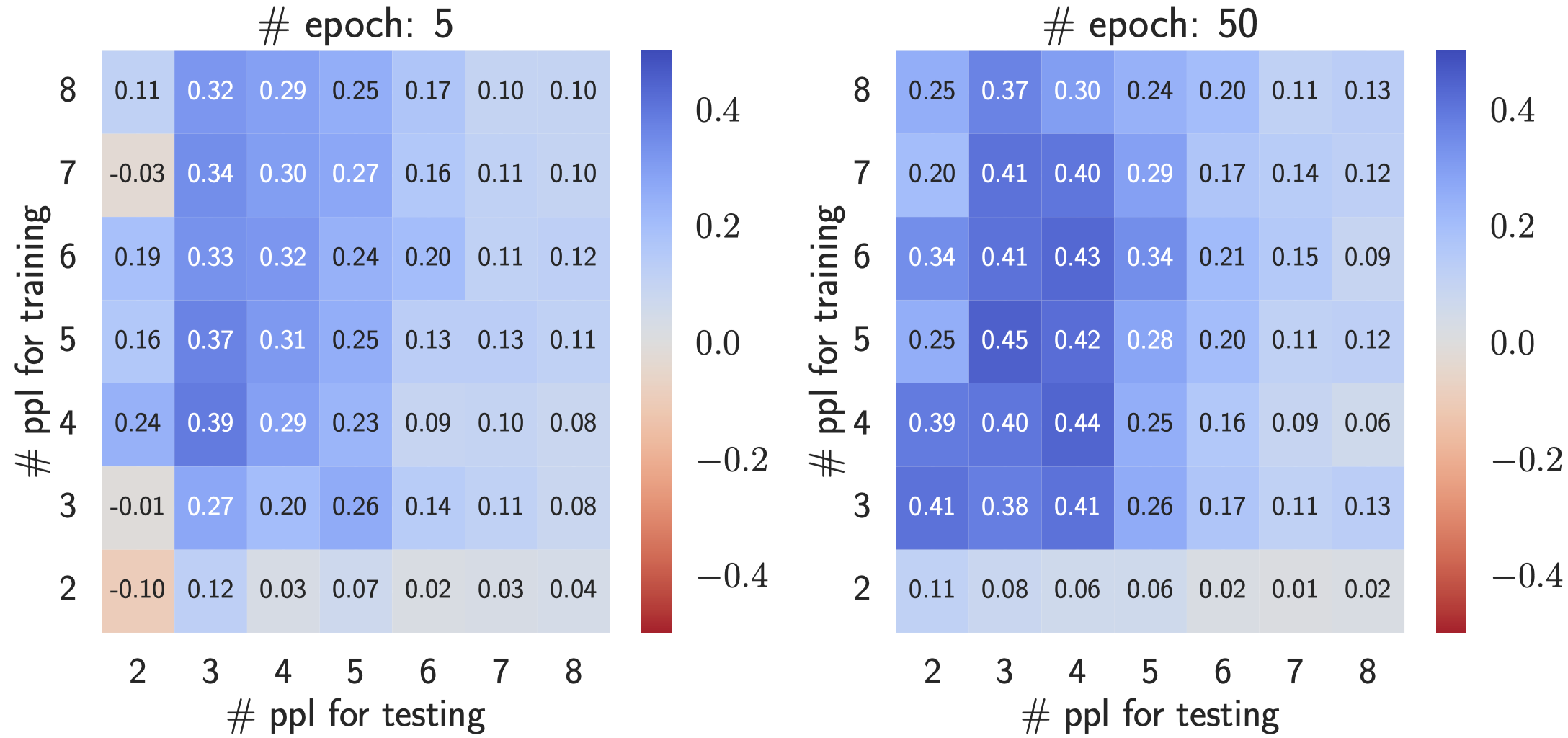
Memorization metric for reasoning tasks

Memorization of LLMs has been studied in various contexts such as privacy, copyright, and knowledge intensive tasks. We focus on measuring memorization when solving reasoning tasks, based on the following characteristic:

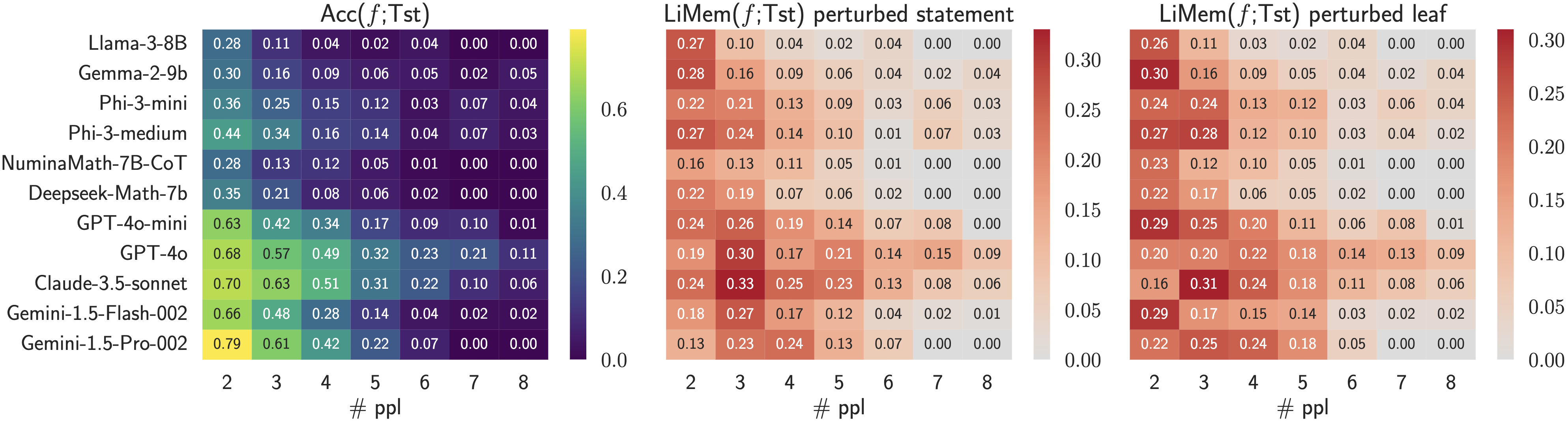
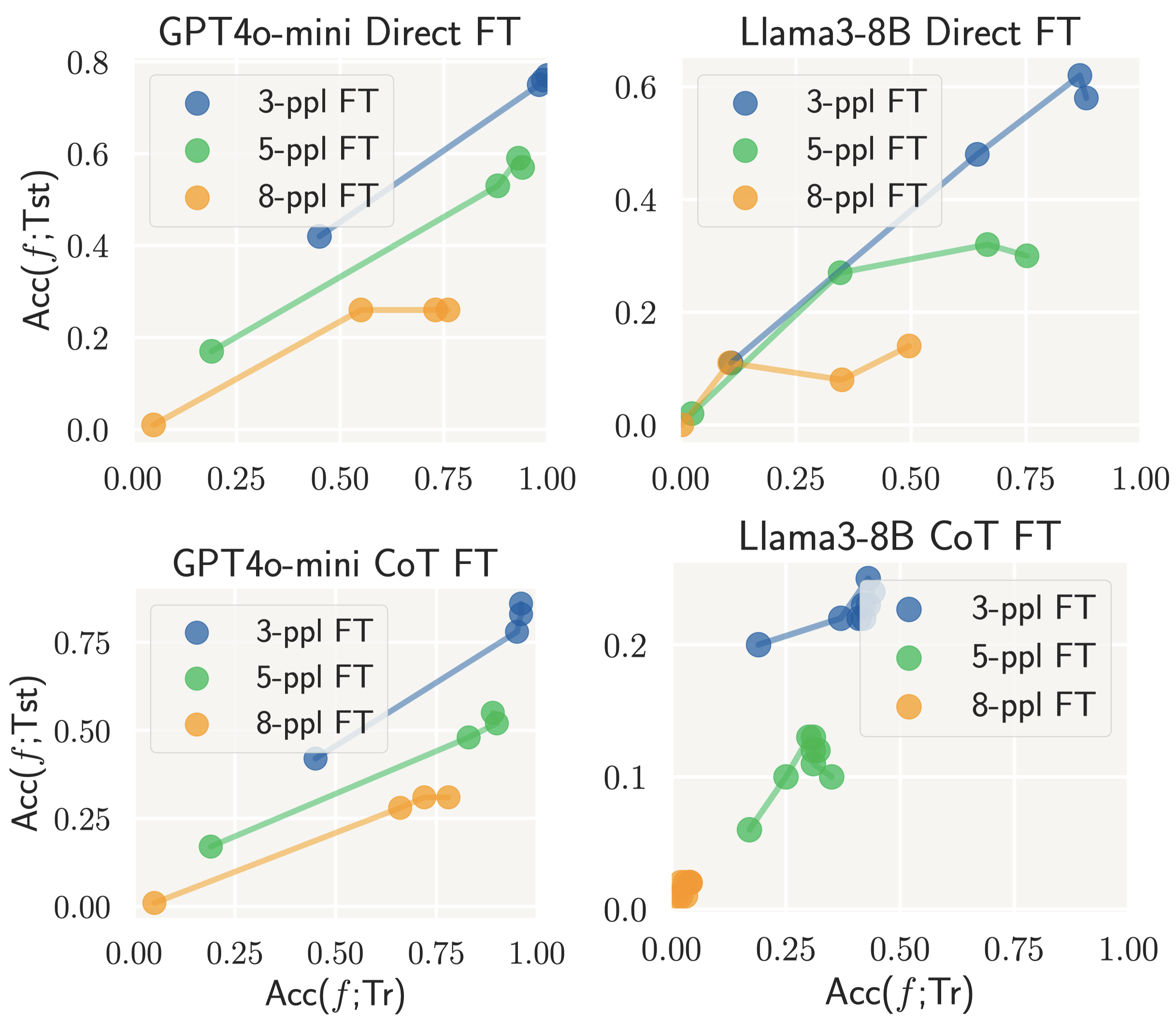
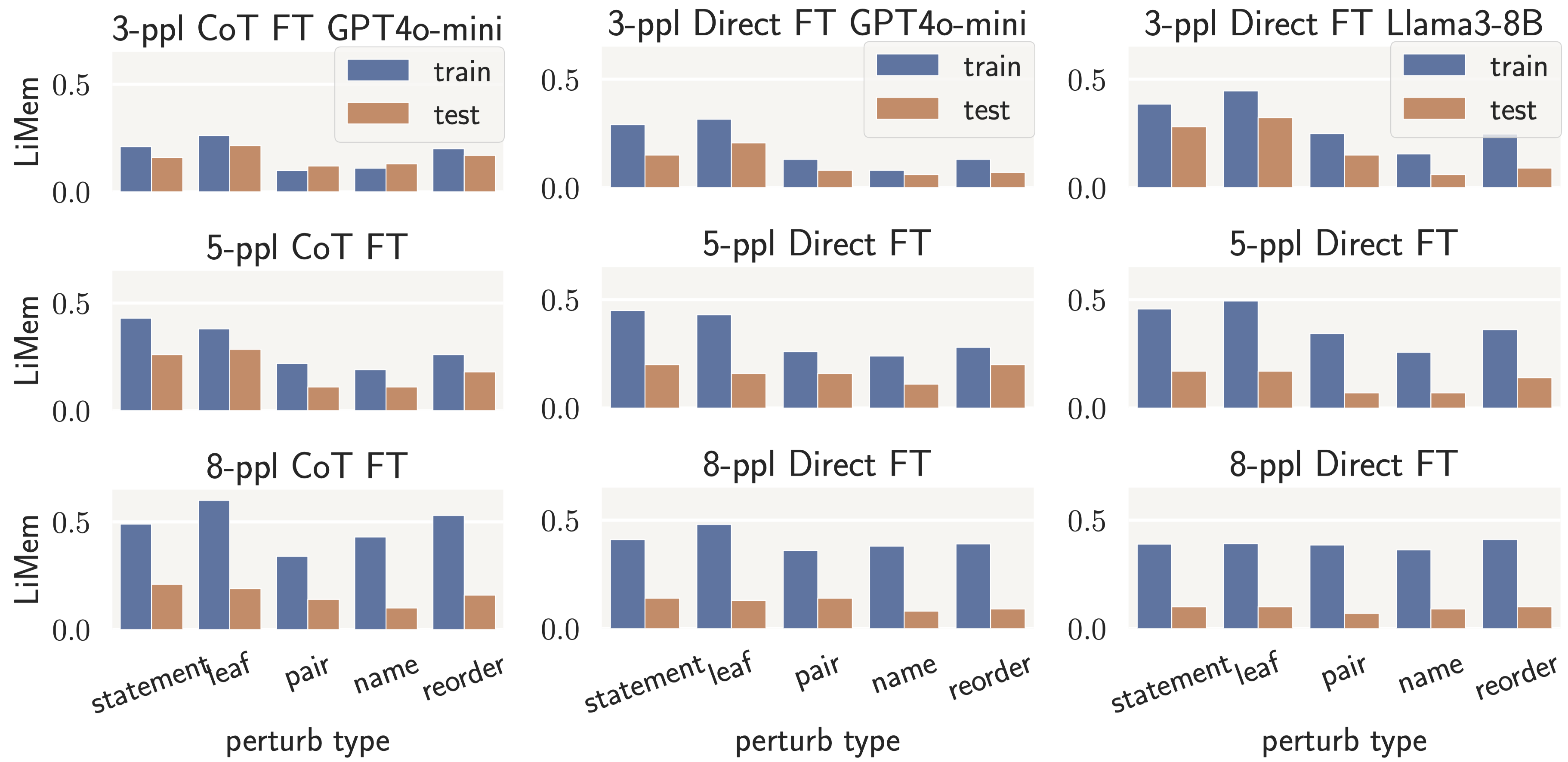
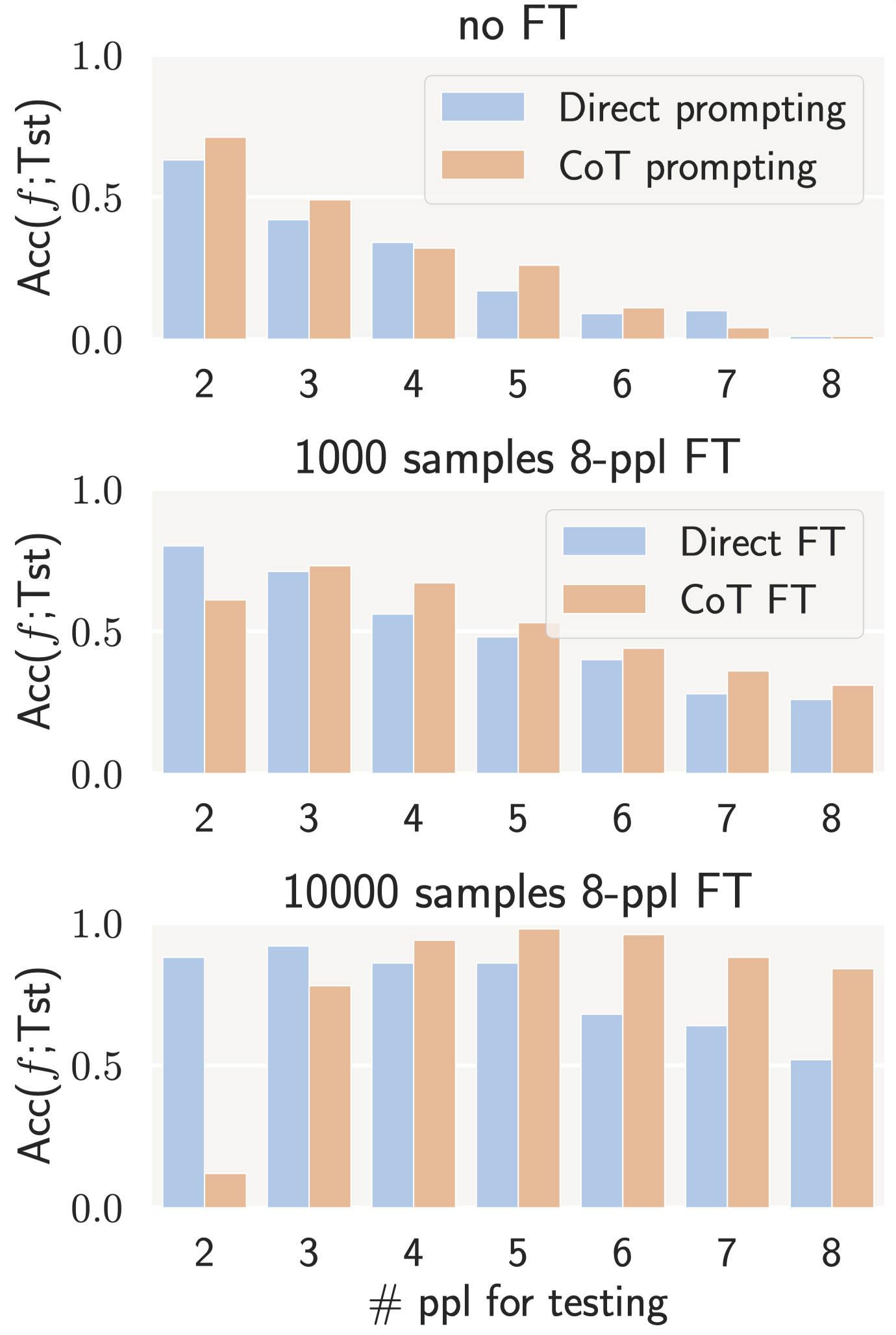
high accuracy on the observed problems (e.g., high \(\mathsf{Acc}(f;\mathcal{D})\) of model \(f\) on training dataset \(\mathcal{D}\));
low accuracy on when the problem is slightly changed (e.g., low consistency ratio \(\mathsf{CR}(f;\mathcal{D})\) between # consistently solved problems after some local perturbations and # solved problems).

Combining above two factors → Local Inconsistency-based Memorization Score: \(\mathsf{LiMem}(f,\mathcal{D})=\mathsf{Acc}(f;\mathcal{D})\cdot(1-\mathsf{CR}(f;\mathcal{D}) )\).

pipeline

Knights and Knaves logical reasoning benchmark

To facilitate our memorization study, we propose a new logical reasoning benchmark that supports automatic problem perturbations.

Knights and Knaves (K&K) (Johnson-Laird & Byrne, 1990) is a type of logical puzzle where some characters tell truth, and others only lie. The goal is to infer each character’s truthfulness. Based on the K&K puzzle, we design a dynamic benchmark that supports:

generating new puzzles with detailed reasoning steps and solutions;

The problem specification, \(N\)-people puzzle, statement depth \(D\), statement width \(W\), defines the problem difficulty.
We support logical statement types including and, or, not, imply, and equivalence.

perturbing a given puzzle locally and recompute the new reasoning steps and solution.

Math-level: replace an entire statement or a leaf node in a statement with a newly sampled one.
Language-level: changing person names (e.g., Oliver/Jacob → Elowen/Osiris), pairs of role names (e.g., knight/knaves → saint/sinner), statements order, and role flipping (e.g., knight/knaves → knaves/knight).

Abstract and natural language modules generate question answer pair and synthetic CoTs for each K&K sample.
Perturbers in these modules can alter the math structure and language description, respectively.

Data Explorer

You can download our data on Hugging Face 🔗.

Quantifying Memorization in LLM Reasoning

From off-the-shelf models to fine-tuned models (finetuning with CoTs and finetuning with answers only).

Off-the-shelf Models

Eval setup: 0-shot direct prompting with task-specific instructions for open-ended question-answering. We create 100 test puzzles for each N-people task.

K&K benchmark poses a challenging logical reasoning task for all off-the-shelf models. Performance drops significantly as the complexity increases (the best accuracy is only 11% for 8-people puzzles).
Off-the-shelf models are sensitive to locally perturbed test samples. When a model has relatively high accuracy, the memorization scores under local perturbation are generally high.

Fine-tuned Models

FT setup: fine-tuning with detailed synthetic CoT steps and answer (CoT FT) and fine-tuning with the answers (Direct FT). We fine-tune the models for each N-people task (1000 training samples) separately.

LLMs interpolate K&K training puzzles

Train & test accuracy increases over the epochs. FTed LLMs can achieve interpolation (≈ 100% train accuracy) for easy tasks, e.g., 3/5-people puzzles.
Llama3-8B struggles with CoT FT, likely due to its limited capacity.

Large memorization scores on training examples

Fine-tuned LLMs exhibit high memorization score on the training set under different perturbations, especially for hard tasks.
Models show stronger memorization under math-level perturbations compared to language-level perturbations.
The memorization score on the test set can be smaller than on the training set.

LLM Learns to Reason by Fine-tuning with Answers Only

Compared to CoT FT, learning from only answers (Direct FT) without detailed reasoning steps is intuitively more challenging, as the models need to come up with the reasoning procedures on their own. It turns out that models can learn to reason K&K puzzles well directly from observing only question-answer pairs.

Reasoning Capabilities of Direct FT-ed Model

Generalization performance increases with memorization level

Test accuracy of FTed Llama3-8B on unseen test set continues to increase over epochs, despite that memorization score on training samples increases.

Fine-tuning with 10k 8-people puzzles

Can brute-force finetuning on a large number of puzzles eventually solve K&K tasks?

10k-FT outperforms 1k-FT across all tasks, reaching ∼ 90% test accuracy on 4/5-people puzzles.
Direct FT with 10k puzzles achieves surprisingly high test accuracy on all tasks. Notably, the transferability to other K&K tasks stems from only learning the answers.
CoT FT is generally more effective than Direct FT.

Fine-tuned model generalizes across different difficulty levels

Test accuracy improvement on N-people problems for FTed LLMs on M-people problems, compared to the un-FTed LLM.

Most grid values are above 0, indicating transferability and enhanced reasoning abilities across unseen eaiser & harder problems.
More training epochs (e.g., 50 vs. 5) improve results, especially for Llama3-8B.

GPT4o-mini CoT FT / GPT4o-mini Direct FT

Llama3-8B Direct FT

Probing Direct FT-ed Model

We use probing techniques (Hewitt & Liang, 2019) to analyze internal representations of Direct FTed models on K&K related tasks, to see whether they develops internal understanding of K&K related reasoning skills when learning only from the answers. The probing task: distinguish correct from incorrect statements in a given puzzle based on the model's intermediate outputs.

Probing accuracy for Direct-FTed Llama3-8B

Probing accuracy for un-FTed Llama3-8B

The near-perfect peak accuracy suggests that the model’s internal representations have a distinction between true/false statements about a given puzzle.
The probing accuracy is much higher than un-FTed model, suggesting that such representations are learned from question-answer pairs during Direct FT.

Distinguishing Memorization from Reasoning

Is there a simple indicator that determines whether a model would solve a given puzzle by reasoning or memorization?

We collect correctly solved training samples by the targeted LLM, and assign a binary categorical label as either “consistently solved” (i.e., solved by reasoning) puzzle or “not consistently solved” (i.e., solved by memorization) puzzle under local perturbation. We train a simple logistic regression model to solve this binary classification problem.

Puzzle-based indicators

We consider text features including TF-IDF, Bag-of-Words, Word Length, Character Length of different text fields of the puzzles.

We observe a best test AUC of 0.629/0.787 for Direct/CoT FT-ed GPT4o-mini, and 0.627 for Direct FT-ed Llama3-8B.
Puzzle-based indicators could be informative, though not perfect, at determining which examples are reasoned vs. memorized.

Model-based indicators

We feed each puzzle question to the FT-ed/unFT-ed model, collect the average embedding at each layer as model-based indicator.

The features from the FTed model are consistently more informative than the un-FTed model, suggesting that the model’s decision regarding memorization vs. reasoning on specific samples likely stems from the fine-tuning process.
The best model embedding-based indicator provides stronger signals than the puzzle-based indicator for Llama3-8B.

Limitations & Discussion

Our results reveal intricate phenomena of the interplay between reasoning and memorization, but challenging questions remain open:

While a model’s reasoning capabilities improve during finetuning as it memorizes more training puzzles, it is unclear exactly how those capabilities develop, especially when fine-tuned on only question-answer pairs without detailed reasoning steps.
While the models’ reasoning capabilities can be significantly improved after fine-tuning, they have not reached 100% test accuracy yet. Is it because the models only learned some “shortcut rules” that can only solve a specific subset of puzzles? If so, what are the shortcuts?
Since some model-based indicators can approximately predict when the model is solving a specific puzzle by memorization vs by reasoning, can we further design intervention mechanisms to bias the model towards reasoning during inference or training time?

If you have any thoughts or are interested in this line of research, feel free to reach out to us.

Acknowledgement

The website layout is based on CotaEval, shared by Boyi Wei. We thank Yuntian Deng, Mingyang Deng, Ziqi Wang, Tiancheng Yu, Mike Mozer, Rishabh Agarwal, Danqi Chen, Matthew Jagielski, Nikunj Saunshi, Wei Xiong and Minghao Chen for their valuable feedback and discussions. Part of this work was completed while Yangsibo Huang was a PhD student at Princeton, and she acknowledges the support of the Wallace Memorial Fellowship and the compute resources at Princeton Language and Intelligence. Bo Li acknowledges the support of NSF No. 2046726, NSF AI Institute ACTION No. IIS-2229876 and the Alfred P. Sloan Fellowship. Any opinions, findings, and conclusions expressed in this material are those of the author(s) and do not necessarily reflect the views of the sponsors.